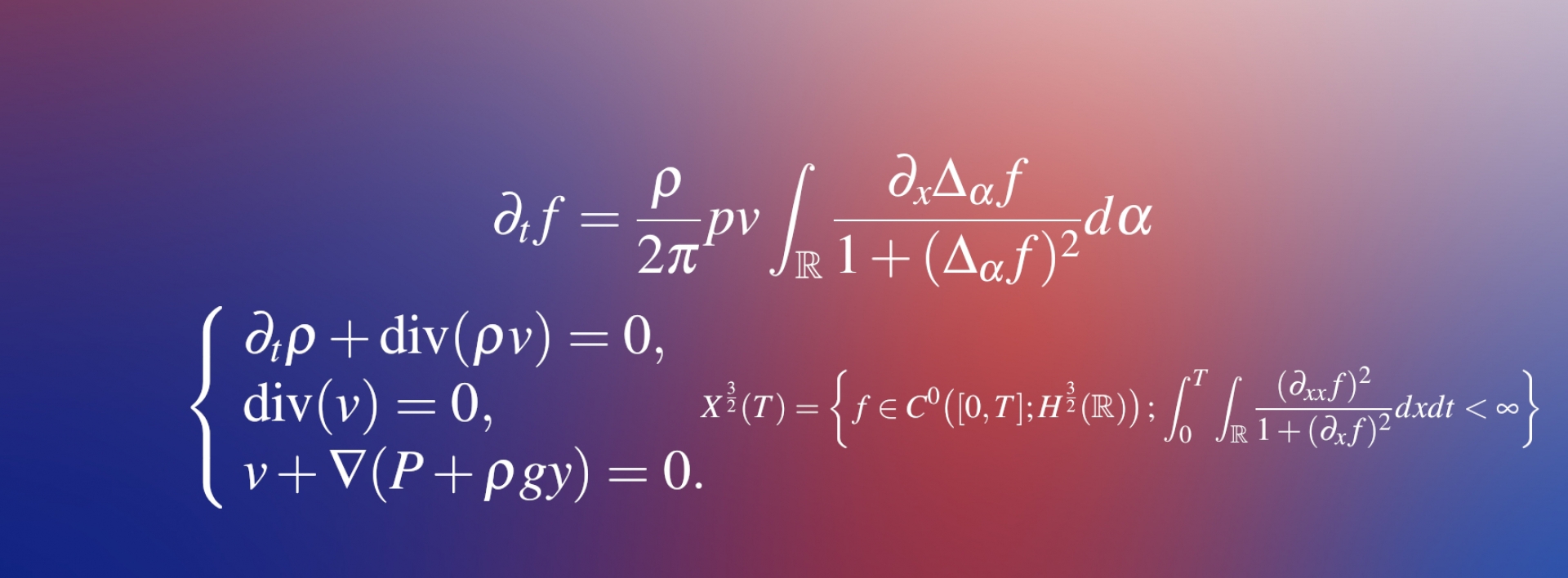Etude de l'équation de Muskat dans le régime critique
Article de référence
T. Alazard, Q.-H. Nguyen. Endpoint Sobolev theory for the Muskat equation. Commun. Math. Phys. 397(3), 1043-1102, 2023.
Un problème issu de la mécanique des fluides
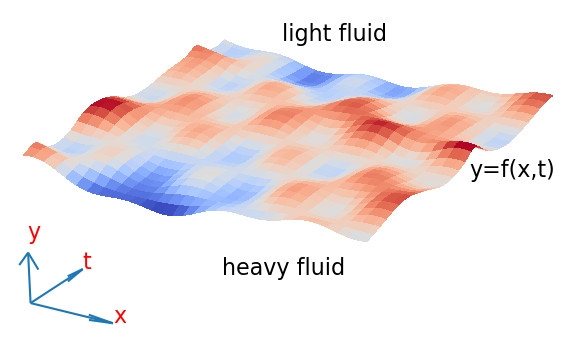
En mécanique des fluides, de nombreux problèmes s'intéressent à l'évolution temporelle de l'interface séparant deux milieux de natures différentes, également connus sous le nom de problèmes à frontières libres. Ces problèmes ont été intensivement étudiés depuis les travaux de Stokes (propagation des vagues) et de Darcy, Hele-Shaw et Muskat (écoulement dans des milieux poreux).
L'équation de Muskat décrit en particulier la dynamique d'une surface séparant 2 fluides incompressibles ayant des densités différentes et obéissant aux lois de Darcy et soumis à la gravité.
Une formulation compacte
Le problème se réduit à un problème de Cauchy pour la paramétrisation f de la surface libre. Les travaux de
- D. Córdoba and F. Gancedo. Contour dynamics of incompressible 3-D fluids in a porous medium with different densities. Comm. Math. Phys., 273(2), 445–471, 2007.
- M. Siegel, R.E. Caflisch, S. Howison. Global existence, singular solutions, and ill-posedness for the Muskat problem. Comm. Pure Appl. Math. 57(10), 1374–1411 (2004)
ont donné une formulation compacte s'exprimant avec des différences finies et des intégrales singulières développées notamment sous l’influence de Calderón, Zygmund et Meyer. Cette formulation très non linéaire peut être étudiée à l'aider d'outils d'analyse harmonique, d’analyse fonctionnelle et d’analyse géométrique relevant de la théorie des EDP non linéaires.
Il est désormais largement prouvé que le problème de Cauchy est bien posé localement en temps dans les espaces de Sobolev de régularité sous-critique, ce qui signifie que la partie linéaire de l’équation domine la partie non-linéaire.
Cas critique
L'article de Thomas Alazard et Quoc-Hu Nguyen se penche sur l'étude de l'équation de Muskat au niveau de la régularité critique, où l'équation change de comportement et devient beaucoup plus difficile à manipuler. Ils prouvent que le problème de Cauchy est bien posé sur l'espace de Sobolov critique H3/2 des fonctions L2 dont les dérivées 3/2 sont également dans L2.
Une difficulté est qu'il n'est pas possible de définir un flot dont la durée de vie serait minoré sur des sous-ensembles bornés de cet espace de Sobolev critique. Pour surmonter cette difficulté et démontrer ce résultat optimal, les auteurs ont estimé les solutions avec une norme qui dépend des données initiales elles-mêmes, en utilisant des laplaciens fractionnaires pondérés introduits dans leurs travaux précédents :
- T. Alazard and Q-H. Nguyen, On the Cauchy problem for the Muskat equation. II: Critical initial data. Annals of PDE, 7(1), 2021.
- T. Alazard and Q-H. Nguyen, On the Cauchy problem for the Muskat equation with non-Lipschitz initial data, Communications in Partial Differential Equation, 46(11),. 2171--2212, 2021.
- T. Alazard and Q-H. Nguyen, Quasilinearization of the 3D Muskat equation, and applications to the critical Cauchy problem, Advances in Mathematics,399, pp 108278, 2022.
Ils ont identifié pour la première fois dans l'équation de Muskat une structure de type-nul dans la non linéarité de l'équation qui cause une dégénérescence de l'opérateur. L'identification de cette structure leur a permis de contourner la difficulté de la dégénérescence. Ils démontrent ainsi un résultat d'existence globale sous des hypothèses de petitesse des données initiales et un résultat de caractère bien posé local pour des données quelconques.
Morris Muskat : un ingénieur
Morris Muskat (1906-1998) était un ingénieur américain travaillant dans l'industrie pétrolière. Il a affiné l'équation de Darcy pour les écoulements monophasés et l'a généralisé pour décrire l'écoulement multiphasique de l'eau, du pétrole et du gaz dans le milieu poreux que constitue une poche réservoir de pétrole.