Geometric tools for life sciences

Thematic overview

• Geometric statistics

As part of her thesis, Elodie Maignant (co-directed with Xavier Pennec), studied the generalization of data reduction techniques by folding to the non-Euclidean case, with applications via Kendall spaces to conformational analysis.

• Metrics and localc geometric actions

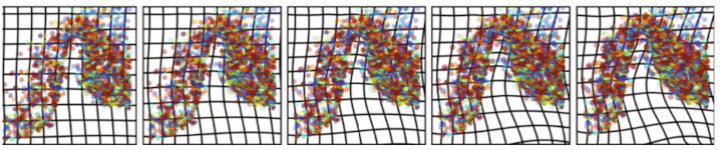
Geodesic trajectories in Riemannian spaces, especially in transport situations, are obviously induced by the choice of metrics and local infinitesimal actions. Despite their usefulness, the overuse of “simple” metrics (such as the L² metric for optimal transport or isotropic Sobolev metrics) can be to the detriment of more natural metrics encoding modeling constraints. Sub-Riemannian approaches in shape spaces open up important avenues with modular approaches decomposing local infinitesimal actions

• Geometric divergences

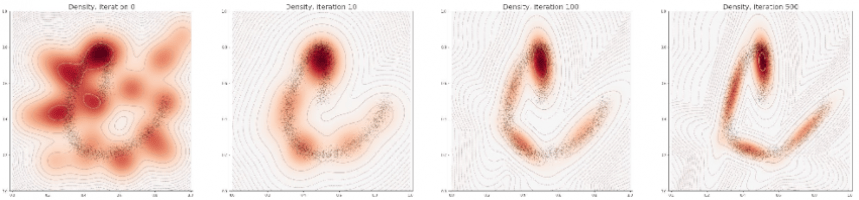
Divergences between probability distributions play a central role in machine learning approaches and as data attachments for spaces of shapes encoded by distributions. Dual kernel norms (or MMDs) provide simple and powerful tools, but optimal transport (OT) approaches are attracting a great deal of interest, particularly since the Sinkhornized version with entropy regularization introduced by Marco Cuturi, albeit at the cost of losing the separation property (it is not a divergence). We have established in Jean Feydy's thesis that this property can be recovered within the framework of a family of Sinkhorn SE divergences that interpolates between MMD and OT as a function of the entropy regularization parameter E.

• Multiscale geometric integration in neuroscience

Spatialized, joint analysis of molecular levels with the macro level of biological tissues and clinical manifestations, in particular with the arrival of spatial transcriptomics techniques (Meshfish, Barseq) with a view to building integrative data-driven models in neuroscience, is very promising but faces a number of challenges. The team is developing a research program around the technological challenges of developing and deploying new methods for acquiring massive data, as well as the mathematical challenges of realigning multi-modal, multi-scale data acquired in weakly consistent coordinate systems and 2-to-2 spatial domains. The first concrete applications on mouse data in the multimodal framework of atlas alignment on 2D data have just been published, and rely heavily on the possibilities offered by KeOps.