Application du transport optimal au transfert de couleur entre images

J. Delon and A. Desolneux, A Wasserstein-type distance in the space of Gaussian Mixture Models, SIAM Journal on Imaging Sciences , Vol. 13(2), pp. 936-970, 2020.

Méthodes rapides de calcul du transport optimal

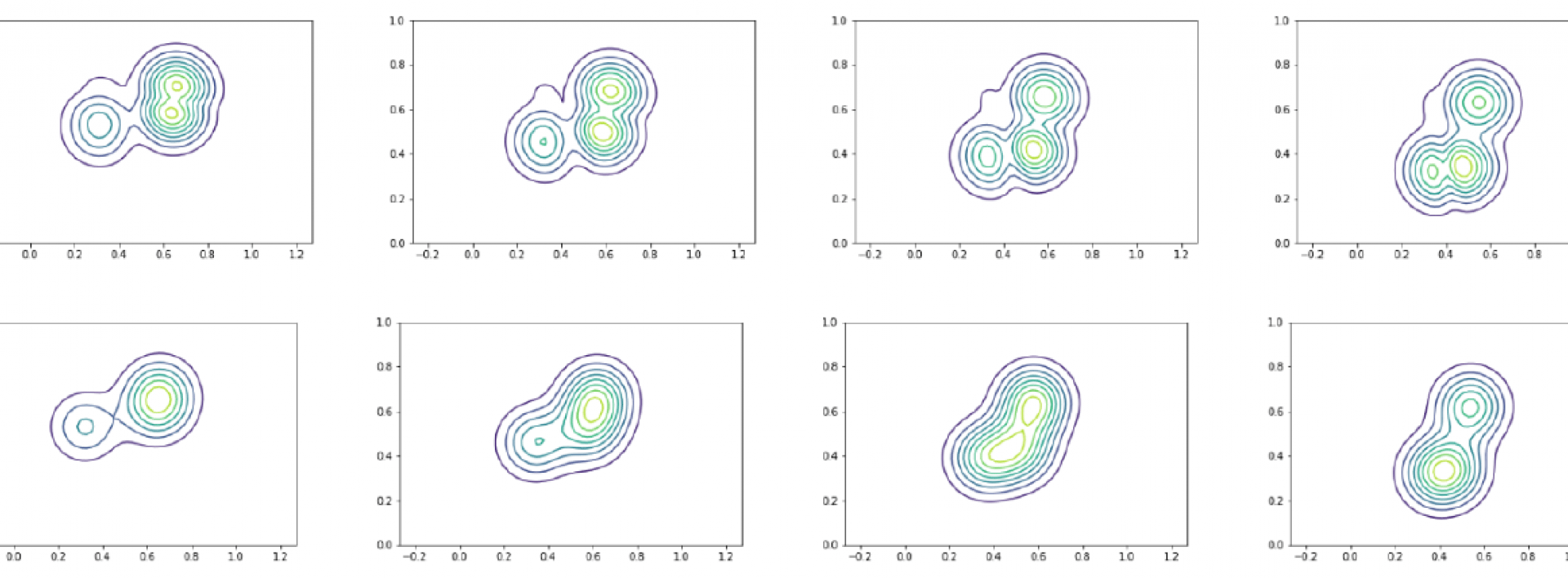
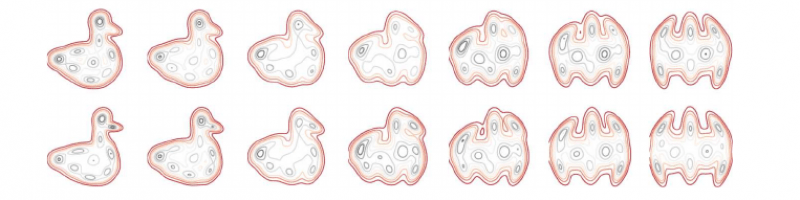
 Le transport optimal est devenu ces dernières années un outil mathématique de première importance en machine learning. Il permet de comparer des distributions entre elles et de les faire se correspondre de manière optimale. Mais le calcul d'un plan de transport optimal est souvent computationnellement très lourd. Plusieurs méthodes ont été développées pour rendre ces calculs plus rapides, et l'article de Julie Delon (médaille d'argent du CNRS 2024) et Agnès Desolneux propose une telle méthode.

Elles y montrent en particulier comment un transport entre mélanges de gaussiennes peut être efficacement calculé en restreignant l'ensemble des couplages possibles à être eux-mêmes des mélanges de gaussiennes. Le problème devient alors discret, de petite taille et donc rapidement résoluble. Une des applications développées est le transfert de couleur entre images.

Extensions

Cet article a donné lieu à de nombreuses extensions : mélanges non nécessairement gaussiens, et surtout extension au transport optimal au sens de Gromov-Wasserstein entre distributions en dimensions différentes.