Outils probabilistes pour le traitement d’images
Présentation de la thématique
Les modèles génératifs d'images
Ces modèles ont connu ces dernières années un essor très important à la fois en termes de modélisation mathématique mais aussi en termes d’applications.
Modèles d'entropie maximale
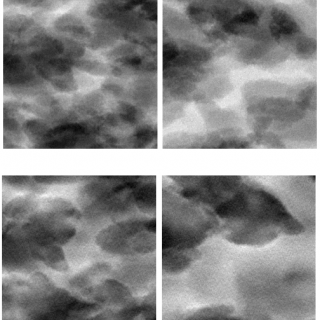
Au cours de la thèse de Valentin de Bortoli, l'équipe s'est en particulier intéressée au problème de la synthèse de textures par des modèles d’entropie maximale sous contraintes satisfaites en espérance. Un algorithme de type dynamique de Langevin a été developpé. Les liens avec les modèles d’entropie maximale où les contraintes sont satisfaites presque sûrement ont été explorés.
Transport optimal
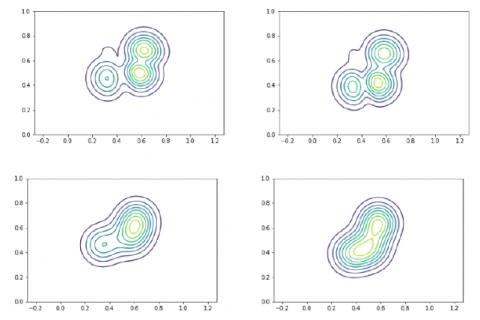
L'équipe utilise également le transport optimal pour la génération d’images. Un résultat obtenu avec Julie Delon montre que le problème du transport optimal entre mélanges de gaussiennes se ramène à un problème de transport discret et de très petite dimension si on contraint les plans de transport admissibles à être eux-mêmes des mélanges de gaussiennes. Ce résultat permet en particulier de faire du transfert de couleur (distribution des couleurs) entre images, ainsi que de la synthèse d’images multiéchelle par transport optimal de la distribution des patchs.
Application en imagerie médicale
Dans un cadre applicatif, un modèle génératif gaussien pour la synthèse de patchs d’images médicales (mammographie) pour de l’augmentation de données et du pré-entraînement pour les méthodes d’apprentissage fédéré a été développé dans la thèse de Gonzalo Quintana (thèse CIFRE GE Healthcare), avec Mathilde Mougeot.
Outils de géométrie stochastique pour l’analyse et la synthèse d’images.
En collaboration avec Hermine Biermé (université de Tours), l'équipe a caractérisé la géométrie (aire, périmètre, caractéristique d’Euler), des images vues comme réalisations d’un champ aléatoire (gaussien ou shot-noise en particulier). Elle s'est attachée à étudier l’effet de la discrétisation des images en pixels sur cette géométrie. La géométrie stochastique et plus précisément les processus ponctuels ont aussi une place importante pour des questions liées au traitement d’images.
Claire Launay (co-dirigée avec Bruno Galerne) a étudié dans sa thèse plusieurs aspects des processus ponctuels déterminantaux (DPP), qui sont des processus ponctuels répulsifs à la fois pour la génération d’images (textures de type shot-noise avec un DPP sur les pixels au lieu d’un processus de Poisson habituellement utilisé), et pour la compression (“résumé”) des patchs d’une image.
Mots clés
Géométrie stochastique ; processus ponctuels ; modèles génératifs d'images ; transport optimal.
Faits marquants
- The mathematics of imaging : Organisation d’un trimestre thématique à l’Institut Henri Poincaré de janvier à avril 2019 avec un programme extrêmement riche : 3 workshops internationaux d’une semaine, 1 pré-école introductive au CIRM, des financements de professeurs invités, des cours doctoraux, et un séminaire hebdomadaire.
- Nombreux exposés grand public autour de la génération d’images et de la géométrie stochastique.
Conférence : Quand le hasard se mêle à la géométrie
Conférence MathEnVille 2023 - Agnès Desolneux

Collaborations
Université Paris-Cité, Université de Poitiers, Université de Tours, GE Healthcare, Google DeepMind
Principales publications
- A. Salmona, V. de Bortoli, J. Delon and A. Desolneux, Can Push-forward Generative Models Fit Multimodal Distributions? , Conference NeurIPS , 2022.
- Z. Li, A.-K. Carton, S. Muller, T. Almecija, P. M. de Carvalho and A. Desolneux, A 3D Mathematical Breast Texture Model With Parameters Automatically Inferred From Clinical Breast CT Images, IEEE Transactions on Medical Imaging , vol. 42, no. 4, pp. 1107-1120, 2023.
- H. Biermé and A. Desolneux, The effect of discretization on the mean geometry of a 2D random field , Annales Henri Lebesgue , Vol. 4, pp. 1295-1345, 2021.
- C. Launay, A. Desolneux and B. Galerne, Determinantal Point Processes for Image Processing , SIAM Journal on Imaging Sciences , Vol. 14, No. 1, pp. 304-348, 2021.
- J. Delon and A. Desolneux, A Wasserstein-type distance in the space of Gaussian Mixture Models , SIAM Journal on Imaging Sciences , Vol. 13(2), pp. 936-970, 2020.